NIOS Class 10th Mathematics (211): NIOS TMA Solution

टिप्पणी :
(i) सभी प्रश्नो के उत्तर देने अनिवार्य है। प्रत्येक प्रश्न के अंक उसके सामने दिए गए हैं।
(ii) उत्तर पुस्तिका के प्रथम पृष्ठ पर ऊपर की ओर अपना नाम, अनुकमांक, अध्यन केन्द्र का नाम और विषय स्पष्ट शब्दो में लिखिए।

1. निम्नलिखित में से किसी एक प्रश्न
का उत्तर दीजिए ।

(a) (i) 3/5 और 4/5 के बीच पाँच परिमेय संख्याएँ
ज्ञात कीजिए।

उत्तर- 3/5= 30/50 , 4/5 = 40/50 अतः

पाँच परिमेय संख्याएँ है : 31/50, 32/50, 33/50, 34/50, 35/50

(ii) क्या सभी धनात्मक पूर्णांकों के वर्गमूल अपरिमेय हैं? यदि नहीं, तो उस संख्या के वर्गमूल का
उदाहरण दीजिए जो एक परिमेय संख्या है।

उत्तर- नहीं, सभी सकारात्मक पूर्णांकों के वर्गमूल आवश्यक रूप से अनिर्घात्मक नहीं होते हैं। किसी सकारात्मक पूर्णांक के वर्गमूल को रेशनल नंबर बनाया जा सकता है जब पूर्णांक सम्पूर्ण वर्ग होता है। उदाहरण के लिए, 4 का वर्गमूल 2 है, और 2 एक रेशनल नंबर है। हालांकि, जो संख्याएँ पूर्ण वर्ग नहीं होती हैं, उनके वर्गमूल सामान्यत: अनिर्घात्मक होते हैं।

(b) निम्नलिखित को सरल कीजिए

(i) 3(a⁴ b³ ) ¹⁰ x 5 (a² b²
) ³

उत्तर- 3(a⁴ b³ ) ¹⁰
x 5 (a² b² ) ³

= 3a^4×10b^3×10×5a^2×3×b^2×3    {∵(a^m)ⁿ=a^mn  , a^m×aⁿ=a^m+n}

=3a⁴⁰b³⁰×5a⁶b⁶

=3×5×a⁴⁰⁺⁶×b³⁰⁺⁶

=15a⁴⁶b³⁶

(ii) (2x ^-2 y ³ ) ³

उत्तर- (2x ^-2 y ³ ) ³  =2³ × x−^2×3×y^3×3 {∵(a^m)n=a^mn   a^m×aⁿ=a^m+n}

                                  =8×x⁻⁶×y⁹=8^x−6y^931/20

2. निम्नलिखित में से किसी एक प्रश्न
का उत्तर दीजिए।

(a) (i) हल करें ( 5m -3 ) / 4 + (3m 2) / 5 = (m + 6)/7

उत्तर–समीकरण को एक कदम के लिए हल करते हैं:

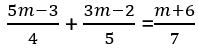
सरल करने के लिए, हमें 4, 5, और 7 के लिए एक सामान्य महत्त्वकर्ण नामकारक ढूंढ़ना है, जो है
4×5×7=140

अब, प्रत्येक पद को सामान्य नामकारक प्राप्त करने के लिए आवश्यक करने वाले कारक से गुणा करें:

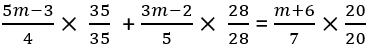
इससे यह होता है:

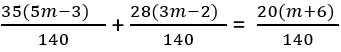
मात्राओं को संयोजित करें:

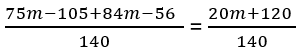
ऐसे ही पदों को संयोजित करें:

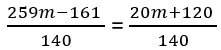
अब, नामकारकों को हटाने के लिए उन्हें गुना करें:

140(259m−161)=140(20m+120)

सरल करें:

259m−161=20m+120

m को अलग करें:

259m−20m=120+161

239m=281

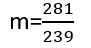
इसलिए, समीकरण का समाधान है
m =281239 

(ii) दो संख्याओं का योग 82 है और उनका गुणनफल 1456 है, दोनों संख्याएँ ज्ञात कीजिए।

उत्तर- दो संख्याओं का योग 82 है और उनका गुणनफल 1456 है, तो इन दोनों संख्याओं को खोजने के लिए हम पहले समीकरणों को हल कर सकते हैं:

1. x+y=82

2. xy=1456

पहले समीकरण से हमें मिलता है कि y=82−x.

इसे दूसरे समीकरण में स्थानांतरित करते हैं:

x(82−x)=1456

सरलीकृत करें और x के लिए हल करें:

82x−x²=1456

x²−82x+1456=0

कोणीय सूत्र या सांख्यिकीय सूत्र का उपयोग करके, हमें मिलता है कि x=32 या x=45.

अगर x=32, तो y=50.

अगर x=45, तो y=37.

इसलिए, दोनों जोड़ों के रूप में दो संख्याएँ हैं (32,50)और (45,37).

(b) बहुपद (x³+ 2x + 1) /5 (7/2) x ² x ⁶ के लिए लिखें

 (i) बहुपद की डिग्री

(ii) x³ का गुणांक

(iii) x⁶  का गुणांक

(iv) अचर पद

उत्तर- प्रदत्त बहुपद है,

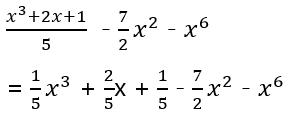
(i) बहुपद का डिग्री उसके शीर्षक का सर्वोच्च डिग्री होता है, जो इस मामले में  है।

(ii)का गुणांक =

(iii) का गुणांक है -6

(iv) अचर पद = 

3. निम्नलिखित में से किसी एक प्रश्न का उत्तर दीजिए।

(a) निम्नलिखित आकृति में, रेखाएँ XY और MN O पर प्रतिच्छेद करती हैं। यदि ∠POY= 90° और  a: b = 2:3 है, तो C ज्ञात कीजिए।

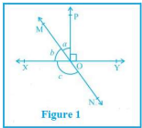
उत्तर-

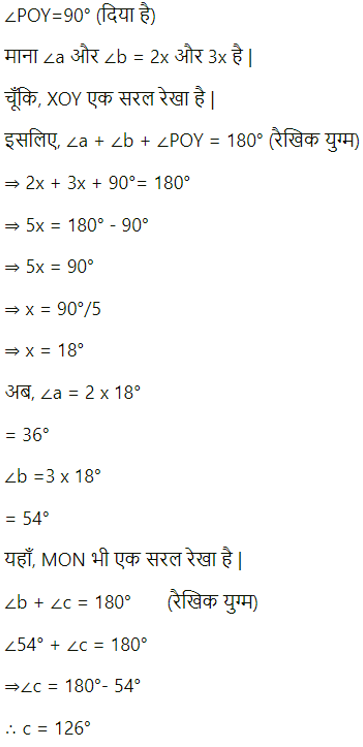
(b) आकृति 1 में ∠PQR= ∠PQR, तो सिद्ध करें की ∠PQS= ∠PRT

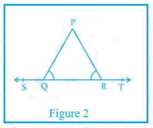
उत्तर-  

4. निम्नलिखित में से किसी एक प्रश्न का उत्तर दीजिए ।

(a) एक समांतर चतुर्भुज के सभी कोण ज्ञात कीजिए यदि एक कोण 80° का है। एक आयत में, एक विकर्ण उसकी एक भुजा से 25° पर झुका हुआ है। दोनों विकर्णों के बीच के न्यून कोण को मापें ।

उत्तर– चौकोर के समांतर चतुर्भुज के आंतर कोणों का योग 360° होता है। एक कोण 80° का है, तो दूसरे कोण का मान होगा:

मान = 180°- 80° = 100°

एक आयत के विकर्ण का मान 90° होता है, इसलिए झुका हुआ विकर्ण:

मान = 90°- 25° = 65°

अब, दोनों विकर्णों के बीच का न्यून कोण:

मान = 180°- (100° + 65°) = 15°

(b) सिद्ध कीजिए कि समांतर चतुर्भुज के कोण द्विभाजक एक आयत बनाते हैं।

एक समलंब ABCD में ABIICD है। यदि ∠A= 55° और ∠B = 70° तो ∠C और ∠D की गणना करें।

उत्तर– समलंब ABCD में, ∠A = 55° (दी गई है), ∠B = 70° (दी गई है)

क्योंकि
ABCD एक समलंब है, इसलिए ∠A = ∠C और ∠B = ∠D

इसलिए, ∠C = ∠A = 55°

और ∠D = ∠B = 70°

5. निम्नलिखित में से किसी एक प्रश्न का उत्तर दीजिए।

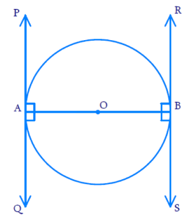
(a) (i) सिद्ध कीजिए कि एक वृत्त के व्यास के सिरों पर खींची गई स्पर्श रेखाएँ समांतर होती हैं।

उत्तर-     

(ii) दो संकेंद्रित वृत्तों की त्रिज्याएँ 5 सेमी और 3 सेमी हैं। बड़े वृत्त की उस जीवा की लम्बाई ज्ञात
कीजिए जो छोटे वृत्त को स्पर्श करती है।

उत्तर-

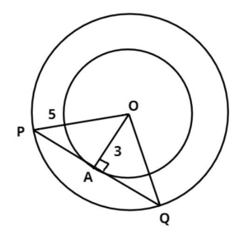
मान लीजिए कि दो संकेंद्रित वृत्त बिंदु पर केंद्रित हैं। और मान लीजिए कि PQ बड़े वृत्त की जीवा है जो छोटे वृत्त को बिंदु A पर स्पर्श करता है। इसलिए, PQ छोटे वृत्त की स्पर्श रेखा है।

OA 1 PQ (चूंकि OA वृत्त की त्रिज्या है)

पाइथागोरस प्रमेय को AOAP में लागू करने पर, हम प्राप्त करते हैं

(b) (i) आकृति 3 में, DE||AC और DF||AE सिद्ध कीजिए कि BF/FE = BE/EC.

उत्तर-

DE||AC और DFI||AE [दिया है। BF सिद्ध करना है: FE BE EC =

ΔΑΒΕ में,

DFIJAE BF BD = FE DA …(1)

ΔАВС में,

DEJJAC BE BD = EC DA …(ii)

समीकरण (1) और (ii) की तुलना करने पर, हमें प्राप्त होता है:

BF BE FE = EC यह सिद्ध हुआ

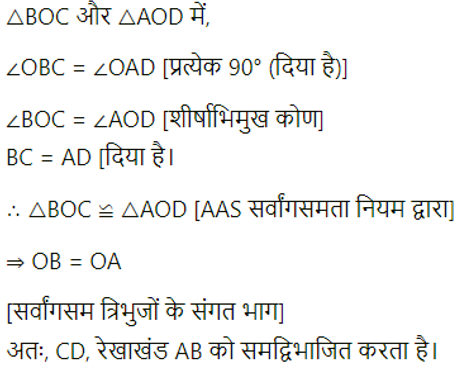
(ii) AD और BC एक रेखाखंड AB पर समान लंब हैं। दिखाइए कि CD, AB को समद्विभाजित करती है।

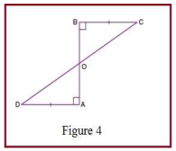
उत्तर-

6. नीचे दी गई परियोजनाओं में से कोई
एक परियोजना तैयार कीजिए ।

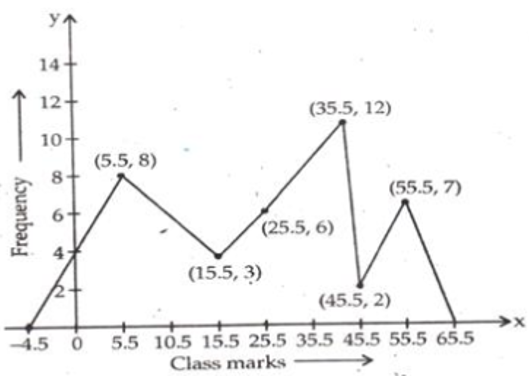
 (a) निम्नलिखित आँकड़ों के लिए आवृत्ति बहुभुज बनाइए-

उत्तर- दिए गए आंकड़ों के लिए एक हिस्टोग्राम बनाएं। हिस्टोग्राम के रेक्टेंगल के शीर्ष के मध्यबिंदु को चिह्नित करें और इन बिंदुओं को रेखा सेगमेंट्स द्वारा जोड़ें। पॉलिगॉन को पूरा करने के लिए, (−10 से 0) और (80 से 90) के दो वर्गों को चिन्हित करें। इन दो वर्गों के मध्यबिंदुओं को रेखा सेगमेंट्स के अंत बिंदु से जोड़ें। ऐसे प्राप्त किए गए कर्व को एक आवृत्ति पॉलिगॉन कहा जाता है।

(b) आठवीं कक्षा के 30 छात्रों के रक्त समूह इस प्रकार दर्ज किए गए हैं:

A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O,

A, AB, O, A, A, O, O, AB, B, A. O, B, A, B, O.

इन आंकड़ों को एक आवृत्ति वितरण तालिका के रूप में प्रस्तुत कीजिए। इन छात्रों में सबसे आम और
सबसे दुर्लभ रक्त समूह कौन सा है?

उत्तर-

रक्त समूह	छात्रों की संख्या
A	9
B	6
O	12
AB	3
Total	30

रक्त समूह AB वाले छात्रों की संख्या = 3

कुल छात्र = 30 

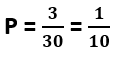
अथवा

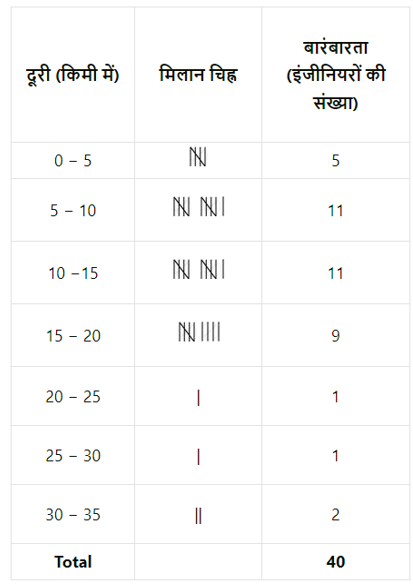
(a) 40 अभियंताओं की उनके आवास से कार्यस्थल तक की दूरी (कि. मी. में) इस प्रकार पाई गई:

पहले अंतराल को 0 – 5 (5 शामिल नहीं) लेते हुए ऊपर दिए गए आंकड़ो के लिए वर्ग आकार 5 के साथ एक समूहीकृत आवृत्ति वितरण तालिका बनाएं। इस सारणीबद्ध निरूपण से आप किन मुख्य विशेषताओं का अवलोकन करते हैं?

उत्तर-  ऊपर दिए गए आँकड़ों को देखकर, एक समूहीकृत बारंबारता बंटन तालिका का निर्माण निम्नानुसार किया जा सकता है।

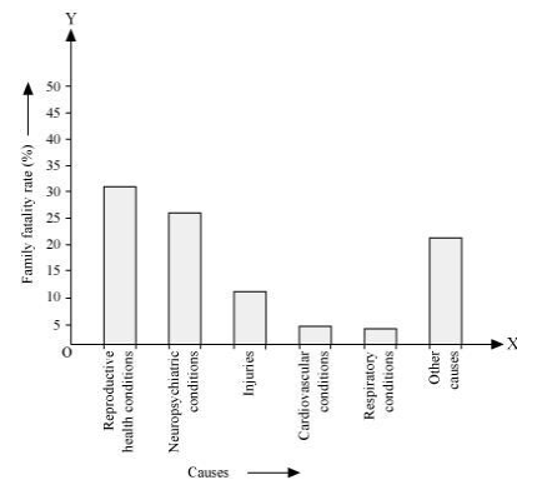
(b) दुनिया भर में 15 से 44 वर्ष के बीच की महिलाओं में बीमारी और मृत्यु के कारण के लिए एक संगठन द्वारा किए गए एक सर्वेक्षण में निम्नलिखित आंकड़े (% में) पाए गए

क्रम संख्या	कारण	महिला मृत्यु दर
1.	प्रजनन स्वास्थ्य की स्थिति	31.8
2.	न्यूरोसाइकियाट्रिक स्थितियाँ	25.4
3.	चोट लगने की घटनाएं	12.4
4.	हृदय संबंधी स्थितियां	4.3
5.	श्वसन की स्थिति	4.1
6.	अन्य कारण	22.0

(i) ऊपर दी गई जानकारी को रेखांकन द्वारा निरूपित कीजिए।

(ii) दुनिया भर में महिलाओं के खराब स्वास्थ्य और मृत्यु का प्रमुख कारण कौन सी स्थिति है?

(iii) अपने शिक्षक की सहायता से किन्हीं दो कारकों का पता लगाने का प्रयास करें जो उपरोक्त
(ii) में प्रमुख कारण होने में प्रमुख भूमिका निभाते हैं।

उत्तर- (i)  

(II) सुरक्षित तथा जनन स्वास्थ्य अवस्था।

(iii) उचित आहार का अभाव, सलाह दी गई अभ्यास की कमी।